RSA 암호에 대해 알아보겠습니다.
RSA 암호는 MIT 공대 연구팀 소속의 Rivest, Shamir, Adleman이 고안해낸 공개키, 비대칭키 방식의 암호화 알고리즘입니다.
공개키 방식이란 말그대로 문서를 받는 쪽에서 모든 사람에게 키를 공개한다는 의미입니다.
비대칭키 방식이란 서로 다른 암호화 키와 복호화 키가 있어서 문서의 송신자와 수신자가 다른 키를 가지는 것을 의미합니다.
RSA 암호화 알고리즘의 전반적인 흐름은 대강 이렇습니다.
- 암호화 키를 모두에게 공개합니다.
- 문서의 송신자가 그 키를 이용하여 보낼 문서를 암호화하여 보냅니다.
- 수신자는 자기가 가진 복호화키로 그 문서를 복호화하여 열람합니다.
더 구체적인 알고리즘을 살펴봅시다.
키 만들기
1) 먼저 두 소수 p 와 q 를 구합니다.
하나의 예로 p = 7, q = 2 라고 합시다.
2) p 와 q 를 곱해서 n 을 구합니다.
위의 예에서 n = 14가 됩니다.
3) Φ(n) = (p-1)(q-1) 을 구합니다.
Φ(14) = 6 * 1 = 6 이 됩니다.
오일러 파이함수를 모르시는 분은 아래 링크를 참고하시기 바랍니다.
4) Φ(n) 보다 작으면서 Φ(n)와 서로소인 e를 구합니다.
e = 5 라고 합시다. 이것이 공개키가 됩니다.
5) e * d ≡ 1 (mod Φ(n))이 되게 하는 d를 구합니다. 물론 d는 Φ(n)과 서로소입니다.
이번 예에서 d 는 5, 11, 17, 23, 29 ... 등이 될 수 있으나 편의를 위해 가장 작은 숫자인 5로 하겠습니다.
이것이 비밀키가 됩니다.
6) 수신자는 (n, e) 를 모두에게 공개합니다.
(14, 5)를 공개합니다.
암호화하기
어떤 송신자가 9 라는 데이터를 수신자에게 안전하게 전달하고 싶어합니다.
송신자는 9의 e제곱을 구해서 모듈러 n값을 구합니다.
95 ≡ 11 (mod 14)
송신자는 수신자에게 11의 암호화된 데이터를 보냅니다.
복호화하기
수신자는 받은 데이터에 다시 d제곱을 해서 모듈러 n 값을 구해 암호화된 데이터를 복호화합니다.
115 ≡ 9 (mod 14)
이렇게 데이터를 안전하게 전달하는 과정이 끝났습니다.
원래 데이터에 e제곱을 해서 d제곱을 했더니 mod n 에서 원래 데이터가 나왔습니다.
이게 도대체 어떻게 된 일일까요?
이에는 수학적인 내용이 들어가 있습니다.
바로 "오일러의 정리"입니다.
"n과 a가 서로소인 양의 정수일 때
aΦ(n) ≡ 1 (mod n) 이다."
왜 이런 명제가 성립하는지 증명이 알고싶다면 아래 글을 참고해 주시기 바랍니다.
이 정리를 관점으로 RSA 암호화 알고리즘을 살펴봅시다.
우리는 처음에 두 소수를 골랐습니다.
예에서는 7과 2라는 작은 숫자를 골랐지만 현실에서 RSA암호를 구현할 때는 150자리 정도되는 큰 두 소수를 고릅니다.
그러면 두 소수를 곱한 값은 대략 300자리 가까이 될 것입니다.
그 정도 크기의 숫자면 사람이 주고받아야 하는 거의 모든 데이터들과 서로소 관계를 이룰 것입니다.
서로소가 아니려면 그 소수와 같거나 그의 배수이어야 할텐데 그러기는 매우 어렵겠죠.
그렇다면 자동으로 오일러 정리의 전제조건이 성립됩니다.
어떤 사람이 보내려는 데이터 a가 있을 때
a ≡ aΦ(n)+1 (mod n)
이 성립할 것입니다.
aΦ(n) ≡ 1 (mod n) 의 양변에 a를 곱한 꼴입니다.
이말은 a 에 Φ(n)+1 를 제곱하면 모듈러 n에서 다시 a가 된다는 말입니다.
이 Φ(n)+1 이 RSA 알고리즘의 핵심이 됩니다.
Φ(n) + 1 = e * d 인 두 숫자 e 와 d 를 구해서 a를 암호화할 때 e 제곱을 하고 복호화할 때 d 제곱을 하면 원래의 a 를 구할 수 있는 것입니다.
우리는 이제 e 와 d 가 어떻게 구해지는지 알아야 합니다. 이때 오일러의 정리가 또다시 이용됩니다.
e * d ≡ 1 (mod Φ(n)) ( e * d 는 Φ(n) 과 서로소)
라는 식이 있을 때 모듈러 연산의 의미상 다음 식과 동치입니다.
e * d -1 = k * Φ(n) (k는 정수)
-1 을 오른 쪽으로 이항하면
e * d = k * Φ(n) + 1
이 됩니다. 이 식만 알면 나머지 e 와 d 는 간단하게 구할 수 있습니다.
Φ(n) 과 서로소인 정수 e 를 하나 정하여 공개키로 삼고
d = (k * Φ(n) + 1) / e
가 성립하는 정수 d를 하나 선택하여 비밀키로 삼는 것입니다.
이리하여 a 에 공개키 e 와 비밀키 d 를 제곱했을 때
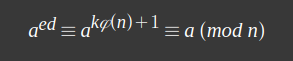
가 성립하므로 원래 값인 a를 얻을 수 있는 것입니다.
우리가 원래 알려고 한것은 Φ(n) + 1인데 k * Φ(n) + 1의 k 는 왜 붙을 수 있는 것이냐 궁금해 하실 수도 있는데
aΦ(n) ≡ 1 (mod n)
에서 양변에 어떤 k 제곱을 하더라도 1k 은 항상 1 이기 때문에 k가 붙든 안붙든 상관이 없습니다.
이렇게 RSA 암호방식의 원리에 대한 설명이 끝났습니다.
RSA 암호의 비대칭키, 공개키 방식은 획기적이었습니다.
모든 사람이 똑같은 하나의 키를 가지는 대칭키 방식과는 다르게
비대칭키 방식은 복호화키를 문서의 수신자만 가지고 있기 때문에 제 3자가 암호문서를 해독하기가 어려웠습니다.
복호화키를 가지지 않은 사람이 문서를 해독하려면
Φ(n) + 1
의 Φ(n) 이 무엇인지 n 을 인수분해해서 알아내야하는데
n 은 보통 300자리 이상의 큰 수이므로 컴퓨터를 사용하더라도 알아내는데 아주 오랜시간이 걸립니다.
현대에는 거의 모든 암호에서 RSA 암호방식이 적용되고 있습니다. 단, 대칭키 방식과 혼합된 형태로 말이죠.
RSA암호방식은 아주 큰 수를 다루므로 컴퓨터의 자원을 많이 소모합니다. 그래서 전달한 문서는 대칭키 방식으로 암호화하고, 그 대칭키를 비대칭키 방식으로 상대방에게 전달하는 것이지요.
오늘은 RSA 암호에 대해 알아보았습니다.
이상 글을 마치겠습니다.