오일러 파이 함수

소수에 대한 오일러 파이 함수

오일러 파이함수는 기호로 Φ(x)와 같이 나타내며 x보다 작으면서 x와 서로소인 자연수의 개수를 의미합니다.

​

예를 들어 소수 7의 경우 7보다 작으면서 7과 서로소인 자연수는

​

{1,2,3,4,5,6} 으로 총 6개 즉,

Φ(7) = 6

입니다.

​

벌써 다 눈치 채셨겠지만 소수는 그 의미상 어떤 수와도 1을 제외한 공약수를 가지지 않으므로 소수보다 작은 모든 자연수들은 그 소수와 서로소일 것입니다.

즉, 오일러 파이 함수는 소수 p에 대하여

Φ(p) = p-1

이 됩니다.

​

자연수 n에 대한 오일러 파이 함수

앞에서 소수 p에 대하여 Φ(p) = p-1이라고 배웠습니다. 그런데 소수가 아닌 경우에는 어떨까요?

​

모든 소수가 아닌 수는 소수들의 곱의 형태로 표현될 수 있습니다.

​

예를 들어 어떤 자연수 a 는

로 표현된다고 하면(p는 소수, k는 자연수)

​

a보다 작은 소수의 개수는 (a보다 작은 모든 자연수) - (a의 약수)라고 할 수 있습니다.

(a보다 작은 모든 자연수) = {1,2,3, ..., a} 이고 (a의 약수) = {p,2p,3p, .. ,a}이므로

​

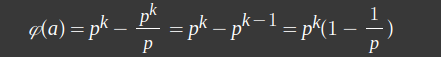
라고 할 수 있습니다.

​

마찬가지로 a가 위와 같이 하나의 소인수가 아닌 여러개의 소인수 즉,

​​

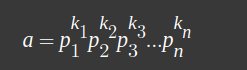
로 표현된다고 할 때, Φ(a)는

 

​

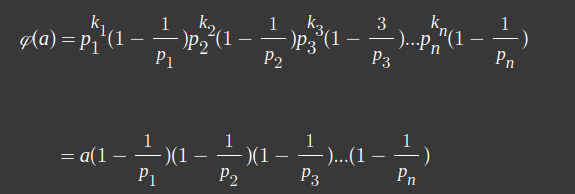
이 됩니다.

​

특히, 두 소수 m,n에 대하여 a = mn 인 특수한 경우에 Φ(a)는

​

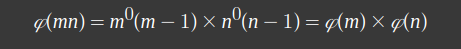
이 됩니다.

​

이상 오일러 파이함수에 대해 알아보았습니다.